Искусственные нейронные сети (ИНС) - сети, в качестве вершин которых выступают искусственные нейроны (ИН). ИНС осуществляет преобразование вектора входных сигналов (воздествий) X в вектор выходных сигналов Y. Интепретация векторов X и Y зависит от постановки решаемой задачи и предметной области. ИНС в настоящее рассматривается как грубая (первого приближения) модель мозга человека и других живых существ. ИНС нашли применение в следующих областях.
Основные достоинства ИНС состоят в следующем:
Освоение материала, посвященного ИНС, требует хороших знаний в области параметрической оптимизации (методов отыскания экстремумов целевой функции). В первую очередь это касается методов оптимизации первого порядка.
Основной строительный блок ИНС - искусственные нейроны. По этой причине рассмотрение материала начинается именно с них.
Считается, что ИН имитирует поведение реальной природной нервной клетки мозга. Упрощенное описание функционирования природного нейрона дано в приложении 1.
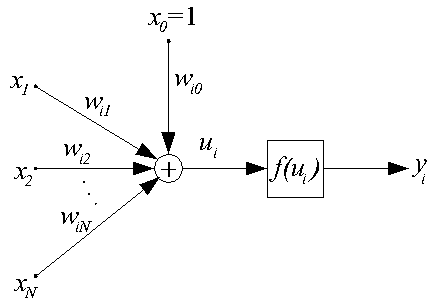
Обощенная схема i-ого нейрона представлена на рисунке.

Здесь X=[x1, x2, ..., xN]T - вектор входных сигналов (воздействий, синапсов (биолог.)) нейрона. x0=1 - константный "псевдосигнал", называемый сигналом поляризации или, просто, поляризатором. В общем случае xj - действительные числа, возможно, размерные, но чаще нормированные. Во многих моделях ИН xj дискретны и могут принимать значения из множеств {0, 1} или {-1, 1}. В некоторых реализациях xj - комплексные числа.
Wi=[wi1, wi2, ..., wiN]T - вектор весов входных сигналов i-ого нейрона (в общем случае, действительные числа). Веса входных сигналов используются для вычисления взвешенной суммы ui входных сигналов i-ого ИН по формуле
Вес wij для размерного входного сигнала xj имеет обратную к нему размерность. Например, если xj имеет размерность [кг], то размерность wij - [кг-1].
Взвешенная сумма входных сигналов ui служит аргументом функции активации ИН f(ui), определяющей значение выходного сигнала yi.
В простейших однослойных (без обратных связей и каскадов) сетях входные сигналы xj нейрона - входные сигналы сети в целом, а выходные сигналы yi нейрона - выходные сигналы сети в целом. В многослойных сетях роль входных сигналов xj некоторых нейронов играют выходные сигналы yi предыдущих слоев ИНС.
Как уже упоминалось ранее, одним из типичных назначений искусственных нейронов и сетей на их основе является классификация и распознавание векторов входных сигналов X. В такой задаче вычисленное по входному вектору X значение yi определяет принадлежность входного вектора тому или иному i-му классу. Например, в качестве значений xj входного вектора могут выступать биометрические данные пациента (температура тела, кровяное давление, концентрация красных кровяных телец в крови и т.п.), тогда выходной сигнал нейрона yi может определять степень уверенности в наличии у пациента болезни Hi.
Понятно, что степень успеха в классификации отдельным ИН и сетью в целом зависит, в общем случае, от "правильности" подбора/назначения весовых коэффициентов wij и коэффициентов функции активации f(ui). Однако, в практических ИНС, как правило, функции активации назначаются однократно и варьированию не подлежат. Таким образом объектом подбора служат только весовые коэффициенты wij.
Для отыскания наилучших с точки зрения решения задачи классификации входных векторов X значений элементов вектора Wi необходимо обучение ИН и ИНС в целом, предваряющее собственно этап классификации. Различают два основных режима обучения: "с учителем" и "без учителя". В первом случае, ИНС предъявляют набор пар векторов <Xk, Dk>, где k - номер пары в наборе (k=1, 2, ..., p). Dk=[dk1, ..., dkM]T - k-ый вектор ожидаемых значений выходных сигналов нейронов (в количестве M), составляющих сеть. Для одиночного ИН M=1. Обучение с учителем предполагает априорное знание о принадлежности векторов входных сигналов различным классам.
Обучение без учителя предполагает предъявление сети ИН (отдельному ИН) "типичного" набора векторов входных сигналов Xk, k=1, 2, ..., p, при этом сеть (отдельный ИН) должна самостоятельно решить задачу кластеризации (определения количества классов и признаков принадлежности к ним).