Задания к лабораторной работе по программированию средствами MPI
Внимание! В данный момент кластер МГТУ извне недоступен
(только с IP-адресов, принадлежащих МГТУ, проверить можно
командой whois). На домашний (локальный) компьютер надо установить
MPICH (ссылка на сайт источника дана ниже).
В Ubuntu наберите команду mpicc и получите подсказку для установки mpich.
Требования к отчету по лабораторной работе приведены в конце страницы.
Внимание! Разработанные программы, решающие дифференциальные
уравнения, должны демонстрировать работоспособность в
"неграфическом" режиме для пространственных
сеток размерностью не менее 10000000 узлов для тысяч временных
слоев. Это, в частности, означает, что недопустимо хранение в ОП всех
результатов для всех временных слоев (шагов интегрирования).
При выполнении данной лабораторной работы используется виртуальный
вычислительный кластер МГТУ.
Для получения терминального доступа к вычислительному кластеру необходимо выполнить команду
ssh user@rk6.clusters.bmstu.ru
, где user - одно из имен student1, student2, ..., student9.
Работать одновременно под одним именем нескольким пользователям настоятельно
не рекомендуется.
Для загрузки на кластер исходных файлов программ необходимо использовать команду
sftp user@rk6.clusters.bmstu.ru
Компиляция и компоновка исполняемого файла прикладной программы выполняется
командой
mpicc -o prg prg.c
Запуск исполняемого файла на 4 узлах кластера по 1 процессу на узел
осуществляется командой
mpiexec -f ~/.machinefile -n 4 ./prg
Перед выходом с кластера обязательно удалить все временные файлы!!!
Для визуализации результатов решения задачи идеально подходит стандартная
для UNIX рутина gnuplot.
Для перенаправления графического вывода gnuplot (и любой другой графической
программы, например, kedit) на экран локальной машины пользователя
необходимо:
- на локальной машине выполнить команду "xhost +" (разрешение
локальному X-серверу принимать запросы от любого узла сети);
- на кластере выполнить команду
"export DISPLAY=localIP:0.0", где localIP -
IP-адрес локальной машины.
Для отладки
MPI-программ в домашних условиях рекомендуется использовать свободную реализацию
стандарта MPI - MPICH [
http://www.mcs.anl.gov/mpi/mpich/download.html].
Литература: Foster I. Designing and Building Parallel Programs. - http://www-unix.mcs.anl.gov/dbpp.
Внимание! Задания, помеченные верхним индексом "*", требуют
изучения теоретического материала
курса "Модели и методы принятия
проектных решений".
1. Разработать средствами MPI параллельную программу решения (численного
интегрирования) одномерной нестационарной краевой задачи методом конечных
разностей с использованием явной вычислительной схемы.
Дан цилиндрический стержень длиной L и площадью поперечного сечения
S. Цилиндричекая поверхность стержня теплоизолирована. На торцевых поверхностях
стержня слева и справа могут иметь место граничный условия первого и второго
родов. Распределение поля температур по длине стержня описывается уравнением
теплопроводности
dT/dt = aT*d2T/dx2+gT
, где
aT=lambda/(CT*p) - коэффициент температуропроводности;
lambda - коэффициент теплопроводности среды;
CT - удельная теплоемкость единицы массы;
p - плотность среды;
gT=GT/(CT*p) - приведенная скорость
превращения тепловой энергии в другие виды энергии, в нашем случае gT=0.
В явной вычислительной схеме МКР для аппроксимации производной температуры
по времени в узле, принадлежащем i-ому временному и j-ому пространственному
слоям, используется "разница вперед":
dT/dt|ij = (Ti+1j-Tij)/ht
Для аппроксимации второй производной температуры по пространственной
координате x используется следующая формула:
d2T/dx2|ij = (Tij+1-2*Tij+Tij-1)/h2x
Тогда алгебраизированное уравнение теплопроводности для узла, принадлежащего
i-ому временному и j-ому пространственному слоям, принимает следующий вид
(gT=0):
(Ti+1j-Tij)/ht
= aT*(Tij+1-2*Tij+Tij-1)/h2x
Такой вид уравнения позволяет в явном виде выразить единственную
неизвестную:
Ti+1j = aT*(Ti
j+1-2*Tij+Ti
j-1)*ht/h2x+Tij
Что, в свою очередь, дает возможность просто организовать вычислительный
процесс в виде "цикл в цикле" (без деталей, связанных с граничными условиями различного рода):
for (i=0; i<n; i++)
for (j=0; j<m; j++)
Ti+1j = ...
Напомним, что значения T0j известны из начальных
условий. Здесь n=Tкон/ht
Требуется разработать параллельную программу, в которой каждый процесс
ответственнен за расчеты для "полосы" расчетной сетки шириной в m/N пространственных
узлов, где N - число процессов.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Методические указания.
2*. Разработать средствами MPI параллельную
программу решения одномерной нестационарной краевой
задачи методом конечных
разностей с использованием неявной вычислительной схемы. Полезно
ознакомиться со следующим материалом.
Временной интервал моделирования и количество (кратное 8) узлов расчетной сетки - параметры программы.
Возможны граничные условия первого и второго рода в различных
узлах расчетной сетки.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Примечание. Использование неявной вычислительной схемы
связано с решением системы ЛАУ на каждом временном слое.
Следовательно, распараллеливание решения краевой задачи неявным методом
сводится к распараллеливанию решения системы ЛАУ методом Гаусса.
Распараллеливание же метода Гаусса проще всего реализуется в ситуации,
когда матрица коэффициентов системы имеет
блочно-диагональный с окаймлением вид.
Матрица же коэффициентов автоматически получит такой вид, если
нумерацию узлов расчетной сетки вести по такой простой схеме:
сначала "внутренние" узлы всех фрагментов, на которые
разбивается стержень, а в последнюю очередь -
"соединительные" узлы. Кстати, сказанное выше справедливо
и для метода прогонки (поскольку этот метод - частный случай метода
Гаусса).
См. также замечание.
3. Разработать средствами MPI параллельную
программу решения двухмерной нестационарной краевой задачи методом конечных
разностей с использованием явной вычислительной схемы.
Объект моделирования -
прямоугольная пластина постоянной толщины.
Подробности постановки подобной задачи даны ниже.
Возможны граничные условия первого и второго рода в различных
узлах расчетной сетки.
Временной интервал моделирования и количество (кратное 8) узлов по осям x и y
расчетной сетки - параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
4*. Разработать средствами MPI параллельную
программу решения двухмерной нестационарной краевой задачи методом конечных
разностей с использованием неявной вычислительной схемы.
Объект моделирования -
прямоугольная пластина постоянной толщины.
Подробности постановки подобной задачи даны ниже.
Возможны граничные условия первого и второго рода в различных
узлах расчетной сетки.
Временной интервал моделирования и количество (кратное 8) узлов расчетной сетки -
параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Примечание. Использование неявной вычислительной схемы
связано с решением системы ЛАУ на каждом временном слое.
Следовательно, распараллеливание решения краевой задачи неявным методом
сводится к распараллеливанию решения системы ЛАУ методом Гаусса.
Распараллеливание же метода Гаусса проще всего реализуется в ситуации,
когда матрица коэффициентов системы имеет
блочно-диагональный с окаймлением вид.
Матрица же коэффициентов автоматически получит такой вид, если
нумерацию узлов расчетной сетки вести по такой простой схеме:
сначала "внутренние" узлы всех фрагментов, на которые
разбивается стержень, а в последнюю очередь -
"соединительные" узлы. Кстати, сказанное выше справедливо
и для метода прогонки (поскольку этот метод - частный случай метода
Гаусса).
См. также замечание.
5*. Разработать средствами MPI параллельную
программу решения одномерной стационарной краевой задачи
методом конечных
разностей. Объект моделирования - стержень постоянного диаметра.
Возможны граничные условия первого и второго рода в различных
узлах расчетной сетки.
Количество (кратное 8) узлов расчетной сетки - параметры программы.
Подробности постановки задачи выяснить у преподавателя.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Примечание. Распараллеливание решения стационарной краевой задачи
сводится к распараллеливанию решения системы ЛАУ методом Гаусса (или
его частным случаем - методом прогонки).
Распараллеливание метода Гаусса проще всего реализуется в ситуации,
когда матрица коэффициентов системы имеет
блочно-диагональный с окаймлением вид.
Матрица же коэффициентов автоматически получит такой вид, если
нумерацию узлов расчетной сетки вести по такой простой схеме:
сначала "внутренние" узлы всех фрагментов, на которые
разбивается пластина, а в последнюю очередь -
"соединительные" узлы.
См. также замечание.
6*. Разработать средствами MPI параллельную
программу решения двухмерной стационарной краевой задачи методом конечных
разностей. Объект моделирования - прямоугольная пластина постоянной толщины.
Возможны граничные условия первого и второго рода в различных
узлах расчетной сетки.
Количество (кратное 8) узлов расчетной сетки - параметры программы.
Подробности постановки задачи выяснить у преподавателя.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Примечание. Распараллеливание решения стационарной краевой задачи
сводится к распараллеливанию решения системы ЛАУ методом Гаусса (или
его частным случаем - методом прогонки).
Распараллеливание метода Гаусса проще всего реализуется в ситуации,
когда матрица коэффициентов системы имеет
блочно-диагональный с окаймлением вид.
Матрица же коэффициентов автоматически получит такой вид, если
нумерацию узлов расчетной сетки вести по такой простой схеме:
сначала "внутренние" узлы всех фрагментов, на которые
разбивается пластина, а в последнюю очередь -
"соединительные" узлы.
См. также замечание.
7*. Разработать средствами MPI параллельную
программу решения методом Гаусса системы линейных алгебраических уравнений, матрица
коэффициентов которой имеет
блочно-диагональный с окаймлением
вид. В качестве тестовых использовать реальные матрицы из
хранилища
или самостоятельно генерировать тестовую СЛАУ описанным ниже
способом.
Размер диагонального блока, ширина окаймления - аргументы программы.
Количество диагональных блоков равно количеству запускаемых процессов.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
См. также замечание.
При реализации обратного хода метода Гаусса недопустимо приведение матрицы к
диагональному виду!
8. Разработать средствами MPI параллельную программу моделирования
распространения электрических сигналов в линейной цепочке RC-элементов
(см. рис. ниже). Метод формирования математической модели - узловой. Метод
численного интегрирования - явный Эйлера. Внешнее воздействие - источники
тока и напряжения. Количество (кратное 8) элементов в сетке, временной интервал
моделирования - параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
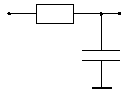 Узловой метод для формирования математической модели электрической системы использует
уравнение второго закона Кирхгофа - сумма токов в узле равна нулю.
Это уравнение для любого i-ого узла в цепочке (кроме крайних) имеет вид
Узловой метод для формирования математической модели электрической системы использует
уравнение второго закона Кирхгофа - сумма токов в узле равна нулю.
Это уравнение для любого i-ого узла в цепочке (кроме крайних) имеет вид
IRл - IRп - IC =0, где
IRл=(Ui-1-Ui)/R
- электрический ток через "левое" сопротивление;
IRп=(Ui-Ui+1)/R
- электрический ток через "правое" сопротивление;
IC=C*dUi/dt - электрический ток через ёмкость;
Ui - электрический потенциал узла с номером i.
Явный метод Эйлера для численного интегрирования ОДУ подразумевает
аппроксимацию производных по времени "разностями вперёд",
поэтому дискретизированное уравнение баланса токов в узле принимает
следующий вид:
(Uni-1-Uni)/R -
(Uni-Uni+1)/R -
C*(Un+1i-Uni)/ht, где
ht - величина шага численного интегрирования.
Из него легко выразить единственную неизвестную величину
Un+1i=(Uni-1-2*Uni
+Uni+1)*ht/(R*C)-Uni
Что, в свою очередь, дает возможность просто организовать вычислительный
процесс в виде "цикл в цикле" (без деталей, связанных с крайними
узлами):
for (n=0; n<N; n++)
for (i=0; i<M; i++)
Un+1i = ...
Напомним, что значения U0i известны из начальных
условий. Здесь N=Tкон/ht
9. Разработать средствами MPI параллельную программу моделирования
распространения электрических сигналов в двумерной прямоугольной сетке RC-элементов
(одномерный аналог которых представлен на рис. выше). Метод формирования
математической модели - узловой. Метод
численного интегрирования - явный Эйлера. Внешнее воздействие - источники
тока и напряжения. Количество (кратное 8) элементов по каждой из осей в сетке, временной интервал
моделирования - параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
10. Разработать средствами MPI параллельную
программу решения уравнения струны методом конечных
разностей с использованием явной вычислительной схемы.
Временной интервал моделирования и количество (кратное 8) узлов расчетной сетки -
параметры программы.
Уравнение струны имеет следующий вид:
d2z/dt2 = a2*d2z/dx2+f(x,t)
, где t - время, x - пространственная координата, вдоль которой
ориентирована струна, z - отклонение (малое) точки струны от положения
покоя, a - фазовая скорость, f(x,t) - внешнее "силовое"
воздействие на струну.
Предусмотреть возможность задания ненулевых начальных условий и ненулевого
внешнего воздействия. Количество элементов в сетке и временной интервал
моделирования - параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
11. Разработать средствами MPI параллельную
программу решения уравнения прямоугольной мембраны методом конечных
разностей с использованием явной вычислительной схемы.
Временной интервал моделирования и количество (кратное 8) узлов по осям x и
y расчетной сетки -
параметры программы.
Уравнение мембраны имеет следующий вид:
d2z/dt2 = a2*(d2z/dx2+d2z/dy2)+f(x,y,t)
, где t - время, x, y - пространственные координаты, z - отклонение (малое)
точки мембраны от положения
покоя, a - фазовая скорость, f(x,y,t) - внешнее "силовое"
воздействие на мембрану перпендикулярное ее плоскости.
Предусмотреть возможность задания ненулевых начальных условий и ненулевого
внешнего воздействия. Количество элементов в сетке, временной интервал
моделирования и количество параллельных процессов - параметры программы.
Программа должна демонстрировать ускорение
по сравнению с последовательным вариантом.
Предусмотреть визуализацию результатов посредством утилиты gnuplot.
При этом утилита gnuplot должна вызываться отдельной командой после
окончания расчета.
Отмечается повальное использование студентами в программах на языке С
для представления прямоугольных матриц конструкций вида
double matrix[N][M];
где N и M - константы.
Этот способ кажется удобным в программировании, поскольку позволяет
адресоваться к элементам матрицы "естественным" способом -
matrix[i][j].
Однако необходимо осознавать, что такому представлению присущ ряд
серьёзных недостатков.
Поэтому в лабораторных работах рекомендуется для хранения прямоугольных
матриц размером NxM использовать одномерный массив:
double *matrix;
. . .
matrix = (double *) calloc (N*M, sizeof(double));
Для доступа к элементу в i-ой строке и j-ом столбце матрицы применяется
конструкция matrix[M*i+j].
При невозможности использования готовых матриц коэффициентов
из хранилища матрицу
коэффициентов и вектор правых частей системы ЛАУ можно сгенерировать
самостоятельно по следующей простой схеме.
-
Положить равными 1 все элементы вектора неизвестных X (это
впоследствии облегчит контроль правильности решения системы ЛАУ).
-
Присвоить всем элементам матрицы коэффициентов A случайные
значения из диапазона, скажем, -1 ... 1.
-
Рассчитать значения всех элементов вектора правых частей B путем
перемножения A и X (при единичном векторе X
перемножение сводится к суммированию элементов строк A).
Внимание! Размерность генерируемых систем не должна быть
"игрушечной", количество неизвестных должно превышать 1000.
Матрица называется блочно-диагональной с окаймлением, если она
имеет следующий вид (здесь Aij - блоки, а не отдельные
элементы).
| A11 | 0 | ... |
0 | A1N |
| 0 | A22 | ... |
0 | A2N |
| ... | ... | ... |
... | ... |
| 0 | 0 | ... |
AN-1,N-1 | AN-1,N |
| AN1 | AN2 | ... |
AN,N-1 | ANN |
Решение методом Гаусса системы ЛАУ с матрицей коэффициентов такой структуры
может быть легко распараллелено.
Во-первых, очевидно, что независимо
друг от друга может быть выполнено приведение к верхнетреугольному
виду в прямом ходе Гаусса диагональных
блоков A11 ... AN-1,N-1 во всех
горизонтальных лентах матрицы (кроме последней).
Во-вторых, параллельно (и это менее очевидно) может быть выполнено
исключение элементов блоков нижнего окаймления
AN1 ... AN,N-1
в том же прямом ходе Гаусса.
В-третьих, очевидно, что после прямого и обратного хода Гаусса по самой нижней
ленте системы ЛАУ, возможно независимое выполнение обратного хода
по каждой оставшейся ленте.
Параллельные программы, предназначенные для решения вычислительных задач
(систем алгебраических и дифференциальных уравнений), должны
продемонстрировать сокращение времени решения.
Для этого, во-первых, необходимо замерять время выполнения программ. Здесь
полезной может оказаться команда time (1). Однако эта команда выдаёт время
выполнения программы целиком, нас же больше интересует "чистое"
время решения без накладных расходов, связанных с генерацией тестовых
матриц, вводом-выводом, подготовкой данных для gnuplot и т.п. Поэтому для
определения времени исполнения отдельных этапов вычислительного процесса
имеет смысл использовать функцию gettimeofday, обеспечивающую точность
замера в 1 мкс. Кроме того удобно обложить #ifdef'ами все фрагменты текста
программы, не связанные непосредственно с целевыми вычислениями.
Во-вторых, для выявления эффекта от распараллеливания необходимо кроме
параллельной версии программы иметь и последовательный вариант. В некоторых
заданиях (например, связанных с МКР) запуск программы в рамках одного потока
или одного процесса MPI даёт временные затраты почти сопоставимые с
затратами последовательной версии. В других (в первую очередь это относится
к решению системы ЛАУ с блочно-диагональной матрицей коэффициентов)
последовательную версию программы приходиться создавать специально. При
многопотоковом программировании параллельная программа легко превращается в
последовательную просто поочерёдным запуском потоков, в случае же
MPI-программы ситуация более сложная.
Внимание. Существует тонкий момент в оценке эффекта от
распараллеливания при решении системы ЛАУ с блочно-диагональной матрицей
коэффициентов. Дело в том, что увеличение (напр., удвоение) количества
параллельно исполняемых потоков/процессов приводит к уменьшению
количества элементов в диагональных блоках (в 4 раза), а, следовательно,
и к уменьшению общего числа ненулевых элементов в матрице коэффициентов.
А это снижение общего числа ненулевых элементов само по себе (без учёта
параллельности) обеспечивает ускорение решения (в идеале, в 4 раза).

